Friday 23 February 2024

Haaland or Bug: Comparing Haaland's stats to Shearer, Kane and Salah

As promised in the update post comparing Shearer, Kane and Salah (https://fulltimesportsfan.wordpress.com/2024/02/14/the-king-his-heir-apparentand-the-pharaoh-waiting-in-the-wings-shearer-kane-and-salah-games-and-goals-per-season-updated-to-the-end-of-the-2022-2023-season/), here is what the the figures look like with Haaland added. 

I'd like to tip my hat to Ted Knutson (@mixedknuts on twitter, other microblogging platforms are available and I'm mostly at @kpfssport@mastodonapp.uk) for the concept of "something or bug", which came from the effect of that year that Burnley really outperformed expectations on Statsbomb’s analyses. Burnley’s data was so different to everyone else’s that after every analysis they had to check whether any outlier was a bug or just Burnley being Burnley. 

I strongly suspected that Erling Haaland's goalscoring stats would have that effect on my graphs but he had such a good first season in the Premiership that I couldn't really say no to L's suggestion when he said "why don't you add Haaland's stats to the analysis?". 

I was right to think Haaland's numbers were going to do terrible, terrible things to my graphs. 

First of all, he's so young that for actual data, there's only numbers up to age 22. For percentage of games played, that makes the data look wild. The percentage of games young players play varies so much depending on circumstance, things like depth of talent at their club, whether they've been loaned out to another club to get some seasoning, whether the coach wants to build them up slowly. So many variables, so it's really messy when you look at data from that age. 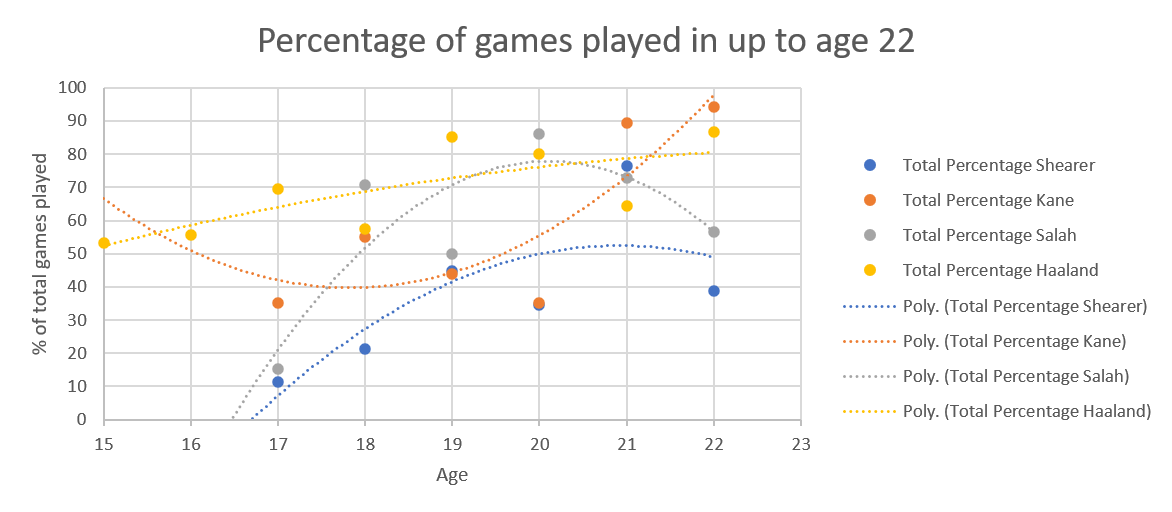Dot plot with the dots joined by dotted lines the same colour as the dots. Blue dots are Alan Shearer, orange are Harry Kane, silver is Mo Salah and yellow is Erling Haaland. The Shearer curve starts at 0, rises to 53 percent at 21 and then drops to 50 percent at 22. The Kane curve is upside down compared to the others because it starts high, at 68 percent, then drops to 40 percent at age 18 and then starts to rise again, finishing at 98 percent at 22. The Salah curve starts at 0, reaches a maximum of 78 percent at 20, and then drops to 58 percent at 22. The Haaland curve meanwhile is more of a steady rise, starting at 52 percent finishing at the highest point of 80 percent at 22.
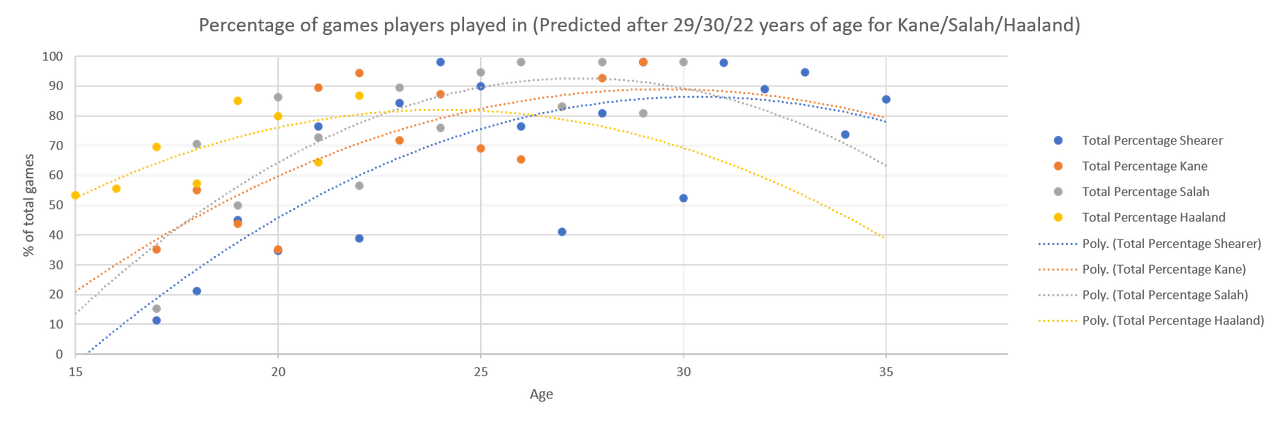
That variability is most clearly seen in Kane's graph, which is upside down compared to the others. Because there's so little real data, the extrapolation in the graph to end of career, 35 years of age because that's when Shearer stopped, particularly effects Haaland's numbers. On the other hand, the extrapolation is needed because everyone's numbers go up after 22.   Dot plot with the dots joined by dotted lines the same colour as the dots. Blue dots are Alan Shearer, orange are Harry Kane, silver is Mo Salah and yellow is Erling Haaland. The Shearer curve starts at 0, reaches a maximum of 86 percent at 31 then drops to 79 percent at 35. The Kane curve starts at 20 percent, rises to a maximum of 89 percent between 29 and 30 years of age, then drops to 80 percent at 35. The Salah curve starts at 15 percent, rises to a maximum of 93 percent between 27 and 28 years of age, then drops to 62 percent at 35. The Haaland curve starts at 52 percent, rises to a predicted maximum of 82 percent at 24 and then drops to 40 percent at 35. 

I think that explains why Haaland's numbers drop so quickly in this graph and I think that'll steady itself with another year's data. I mean, according to this, his numbers max out at 24 and, barring injury (and may he be kept from those) that doesn't reflect footballing truth. 

The goals per game up to the oldest point all four players have reached is another one bent and mangled by lack of data. 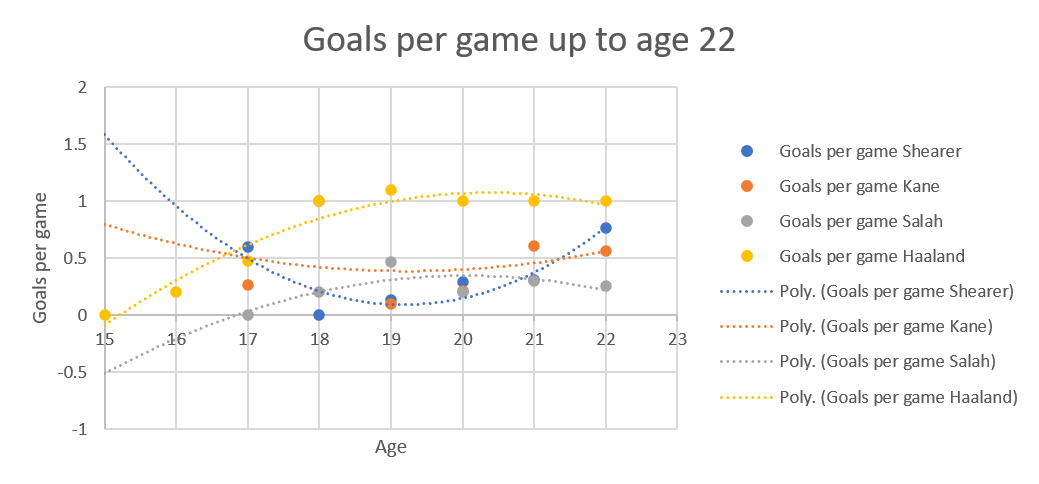Dot plot with the dots joined by dotted lines the same colour as the dots. Blue dots are Alan Shearer, orange are Harry Kane, silver is Mo Salah and yellow is Erling Haaland. The Shearer curve starts at 1.6 due to a nonsense of extrapolation. It drops to a minimum of 0.1 goals per game at 19 then rises again to 1.75 at 22. The Kane curve starts at 0.8, again due to extrapolation, reaches a minimum of 0.4 goals per game between 19 and 20, then rises to 0.55 goals per game by 22. The Salah curve starts at 0.5, rises to a maximum of 0.4 at 20 then drops slightly to 0.3 at 22. The Haaland curve starts at 0, reaches a maximum of 1.1 between 20 and 21, then drops slightly 1 goal per game at 22. That's two upside down curves versus two right way up curves, because of the extrapolation needed because Haaland started in the adult leagues earlier than the others. 

Also, this was all while Salah was still a winger, which explains his low numbers. 

On the other hand, you can imagine the nonsense extrapolation makes of Haaland's numbers if you send them forward to him being 35.

Behold, the nonsense: 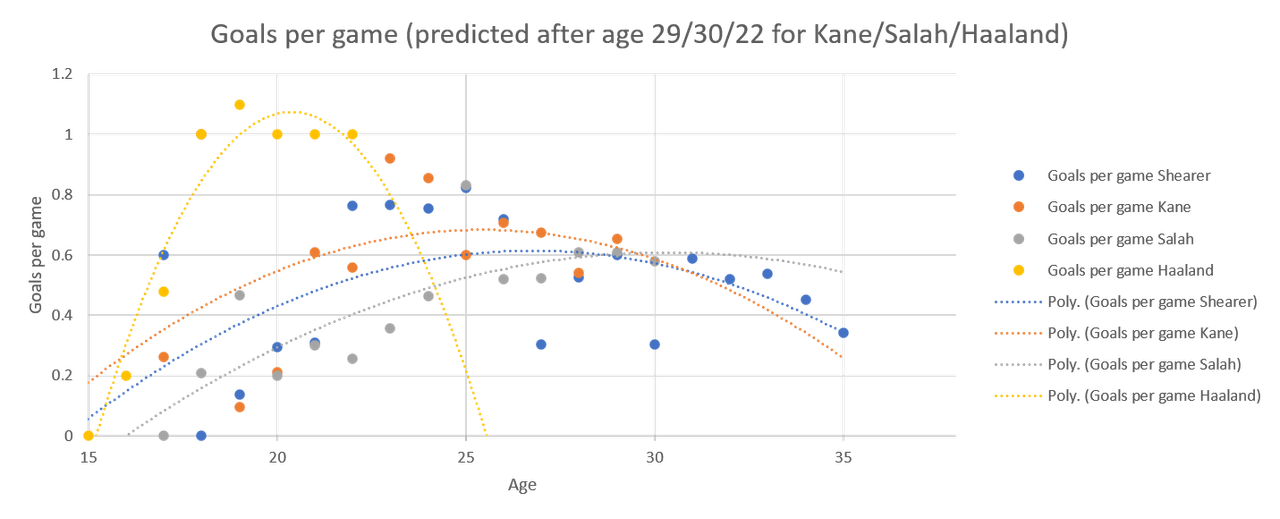  Dot plot with the dots joined by dotted lines the same colour as the dots. Blue dots are Alan Shearer, orange are Harry Kane, silver is Mo Salah and yellow is Erling Haaland. The Shearer curve starts at 0.6 goals per game, rises to a maximum of 0.6 goals per game at 27, then drops to 0.35 at 35. The Kane curve starts at 0.19, rises to a maximum of 0.7 between 25 and 26, then drops to 0.26 at 35. The Salah curve starts at 0, rises to a maximum of 0.6 at 30, then drops to 0.37 at 35. The Haaland curve starts at 0, rises sharply to maximum of 1.05 between 20 and 21 then drops back to 0 by 26. According to the nonsense, Haaland stops scoring at 26. Again, may he be kept from injury, that is clear nonsense. 

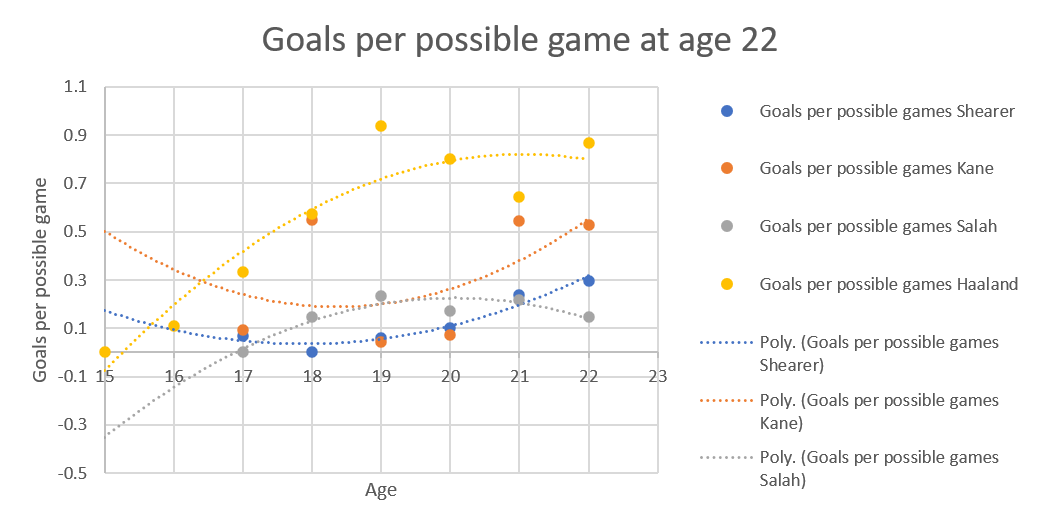
For goals per possible game, up to the oldest age all of them have achieved, we're back in the land of the banana curve, due to extrapolation. Dot plot with the dots joined by dotted lines the same colour as the dots. Blue dots are Alan Shearer, orange are Harry Kane, silver is Mo Salah and yellow is Erling Haaland. The Shearer curve starts at about 0.19, drops to a minimum of 0.05 at 20 years of age, then rises to 0.3 goals per possible game at 22. The Kane curve starts at 0.5 goals per possible game, drops to a minimum of 0.2 between 18 and 19, then rises to 0.54 goals per game at 22. The Salah curve starts at -0.35 goals per game, I blame extrapolation, then rises to a maxium of 0.21 at 20, then drops to 0.15 goals per possible game at 22. The Haaland curve starts at -0.1 goals per possible game, rises to a maximum of 0.82 goals per possible game at 20 then drops slightly to 0.8 goals per possible game at 22. Again, it's Kane and Shearer who are banana shaped, and Salah's goals per possible game is lower than everyone else's because he was still a winger. 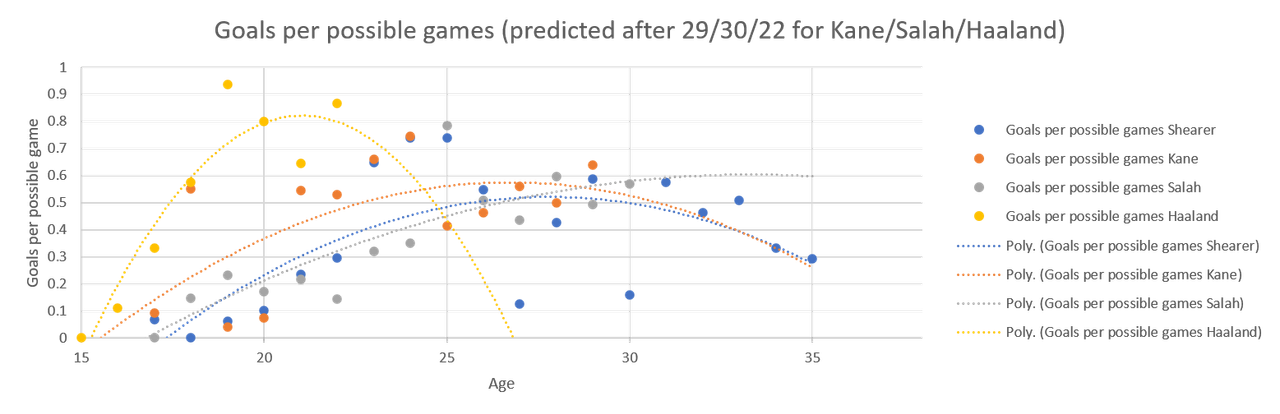Dot plot with the dots joined by dotted lines the same colour as the dots. Blue dots are Alan Shearer, orange are Harry Kane, silver is Mo Salah and yellow is Erling Haaland. The Shearer curve starts at 0 goals per possible game, up to a maximum of 0.5 goals per possible game between 27 and 28, then drops to 0.29 goals per possible game at 35. The Kane curve starts at 0, rises to a maximum of 0.58 goals per possible game between 26 and 27 and then drops to 0.28 at 25. The Salah curve starts at 0, then rises to a maximum of just over 0.6 at 33 before dropping just below 0.6 goals per possible game at 35. The Haaland curve starts at 0, before rising to a maximum of 0.83 at 21, before dropping like a stone to 0 at 27. Again, Haaland's is that shape due to a lack of data. 

It'll be interesting to see the shape of his curve change next year.
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)