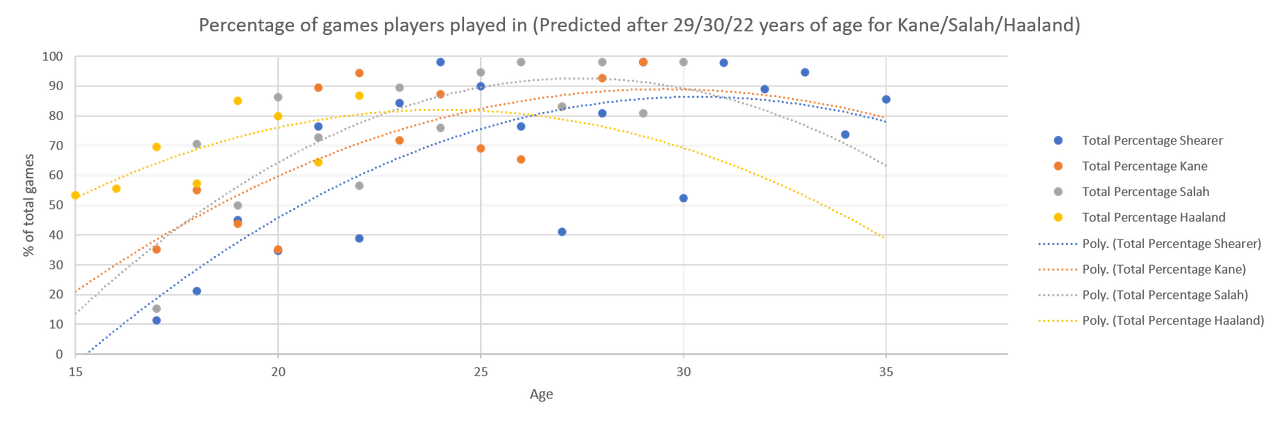
 That's two upside down curves versus two right way up curves, because of the extrapolation needed because Haaland started in the adult leagues earlier than the others.
That's two upside down curves versus two right way up curves, because of the extrapolation needed because Haaland started in the adult leagues earlier than the others. 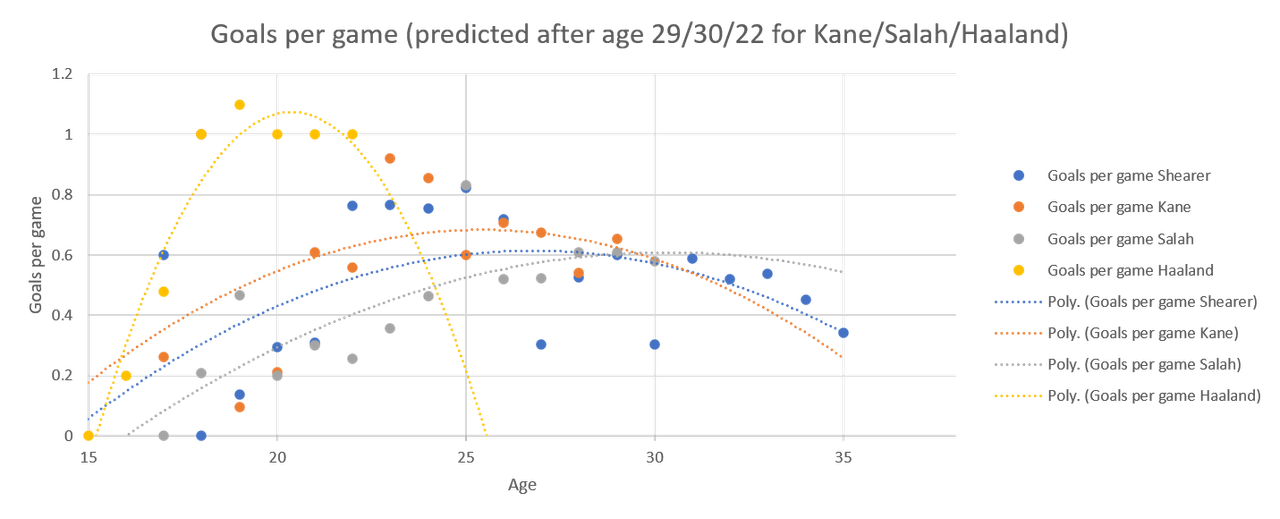
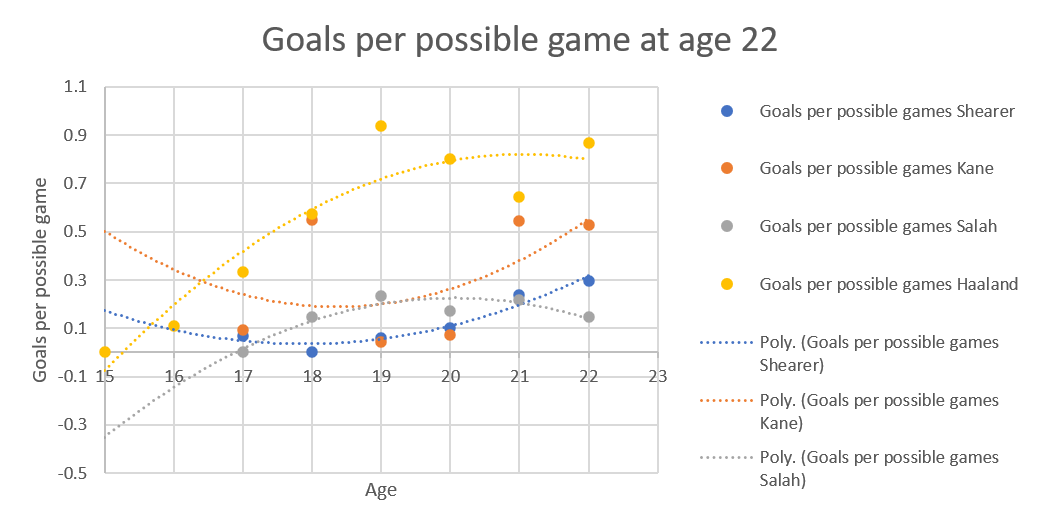


 That's two upside down curves versus two right way up curves, because of the extrapolation needed because Haaland started in the adult leagues earlier than the others.
That's two upside down curves versus two right way up curves, because of the extrapolation needed because Haaland started in the adult leagues earlier than the others. 


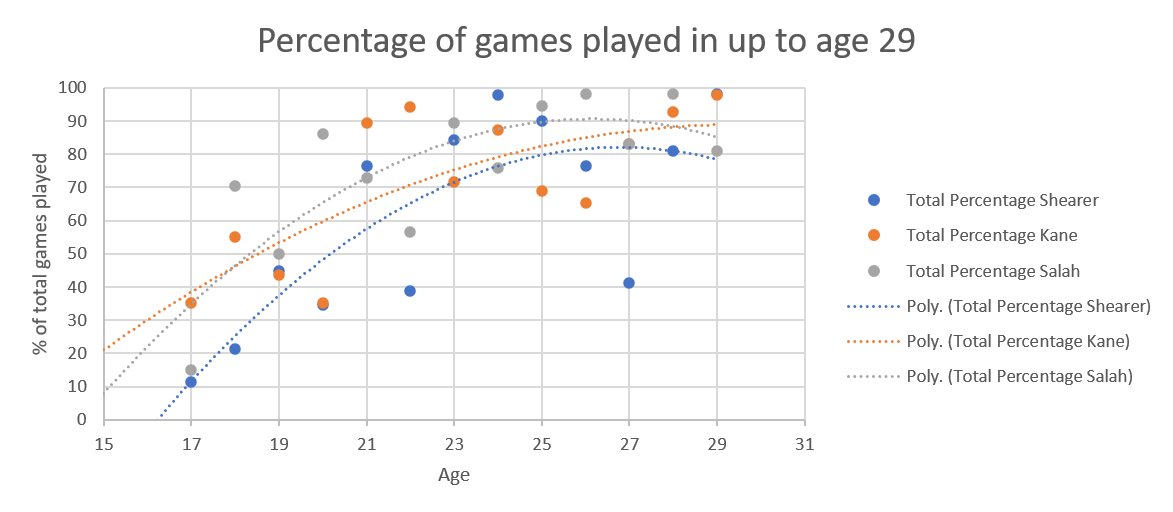
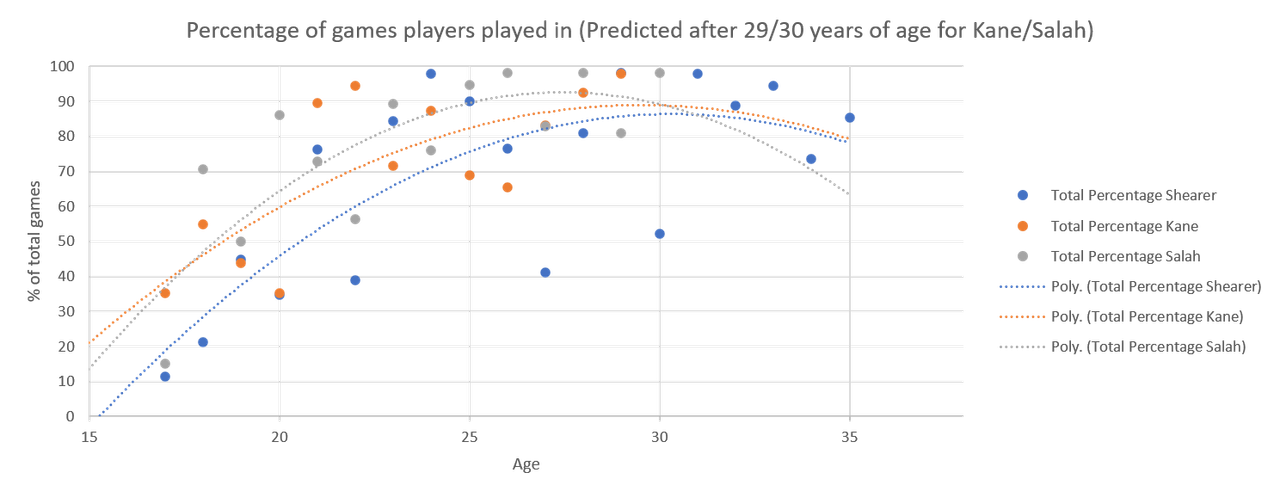
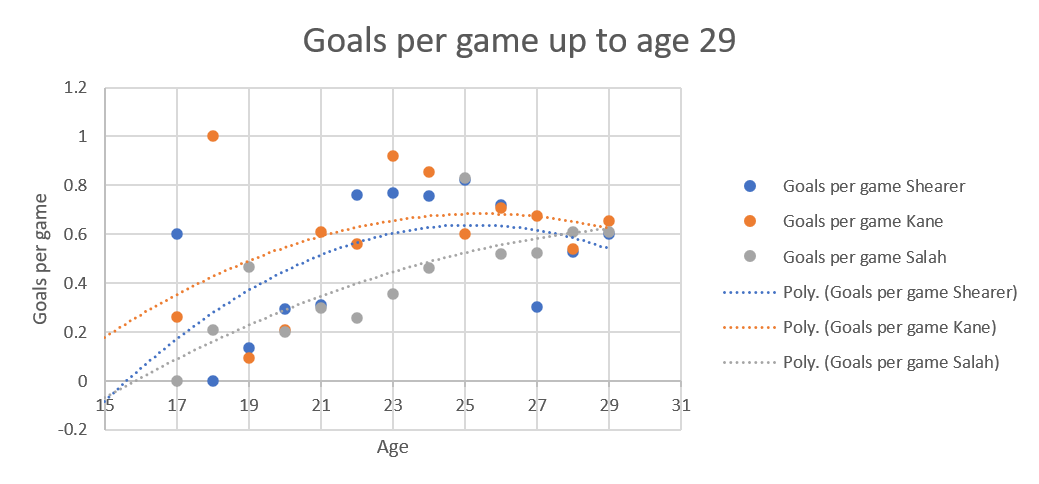


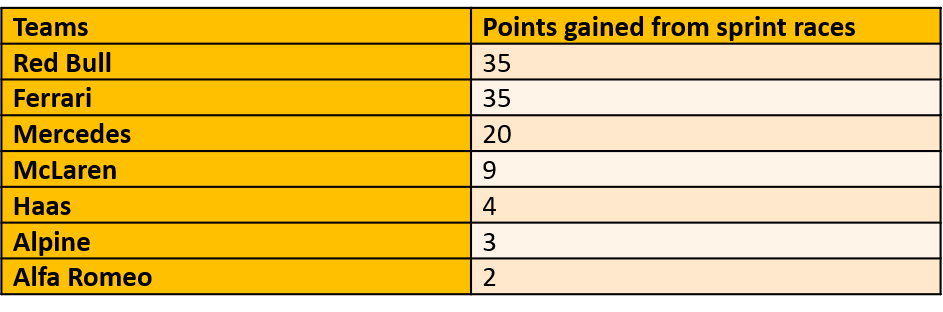

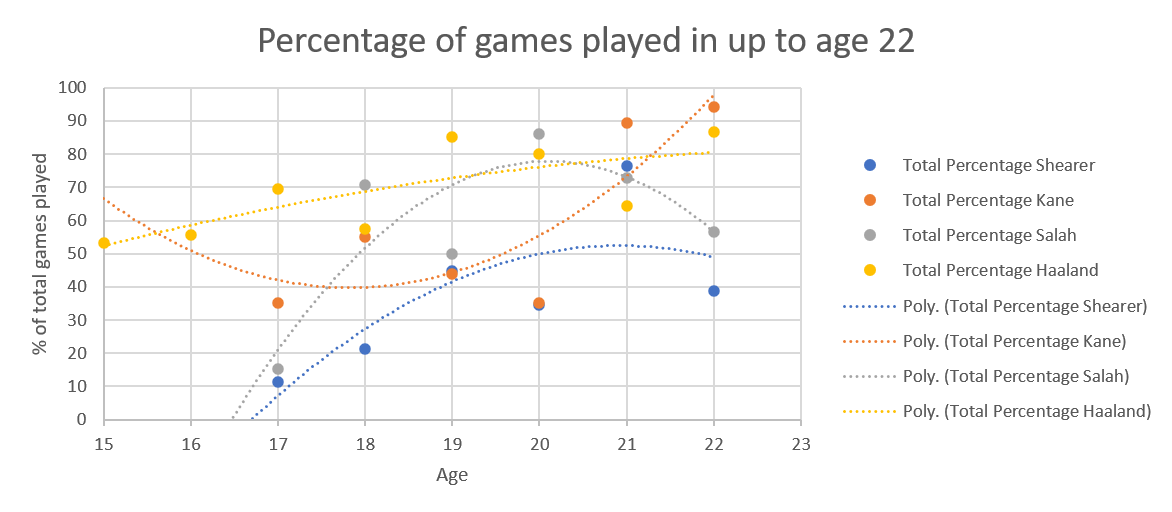
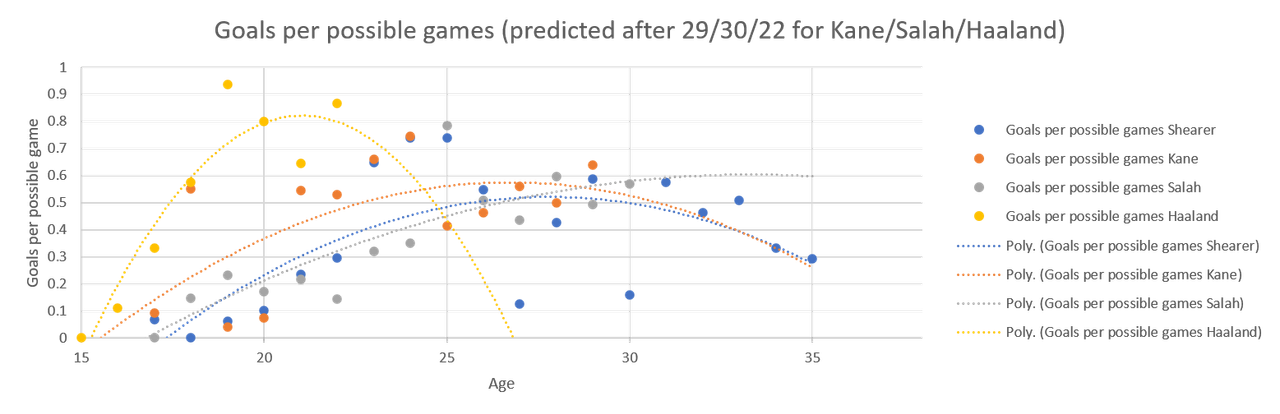
 Obviously, for Shearer (blue dots and dotted line) we had stats for his whole career. The noticeable thing is that even at the end of his career, he was playing in a high percentage of Newcastle's games (in his last year he played in 85% of Newcastle’s games), but this might have been because Newcastle really never had a replacement for Shearer ready at the time.
Obviously, for Shearer (blue dots and dotted line) we had stats for his whole career. The noticeable thing is that even at the end of his career, he was playing in a high percentage of Newcastle's games (in his last year he played in 85% of Newcastle’s games), but this might have been because Newcastle really never had a replacement for Shearer ready at the time. 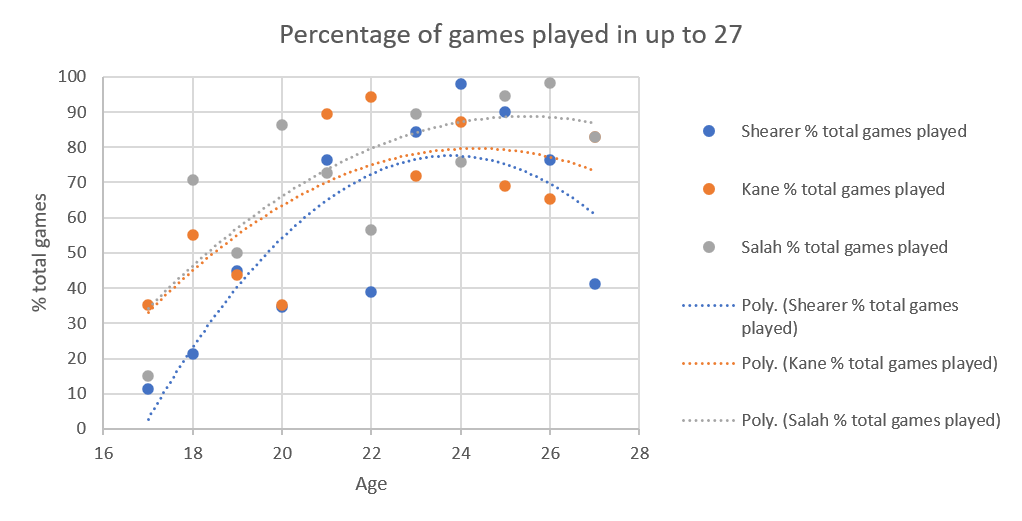
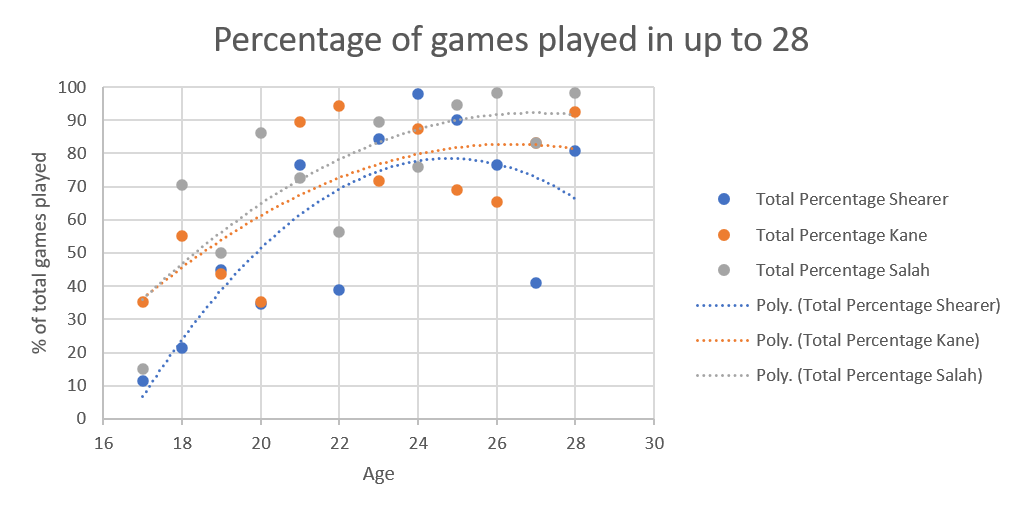
 The two lower blue dots for Alan Shearer, at 27 and 30 years, reflect the years he had his worst injuries, which does suggest that injuries also reduce potency as you come back.
The two lower blue dots for Alan Shearer, at 27 and 30 years, reflect the years he had his worst injuries, which does suggest that injuries also reduce potency as you come back. 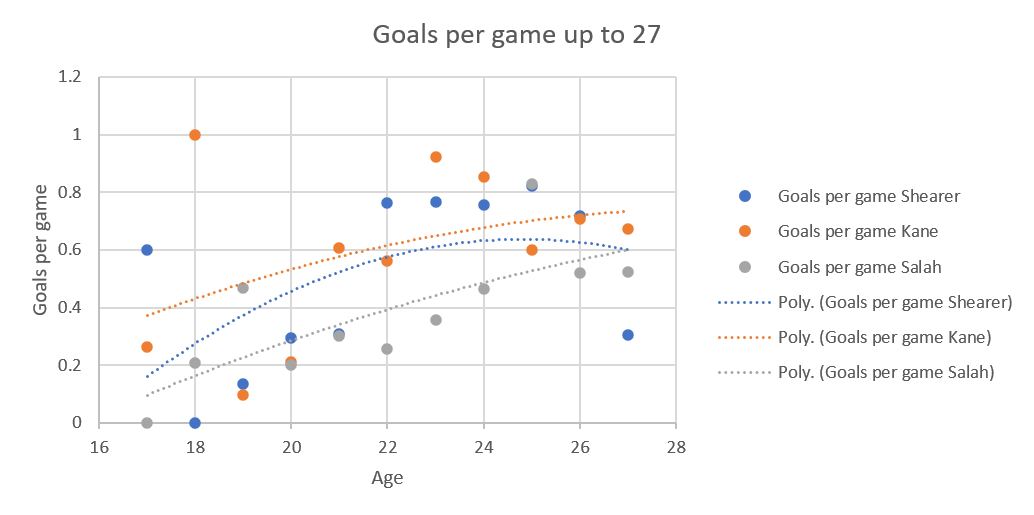 The really interesting thing is that Salah's curve has a completely different shape to the other two, possibly reflecting his change from winger to striker, whereas the other two have always been strikers.
The really interesting thing is that Salah's curve has a completely different shape to the other two, possibly reflecting his change from winger to striker, whereas the other two have always been strikers.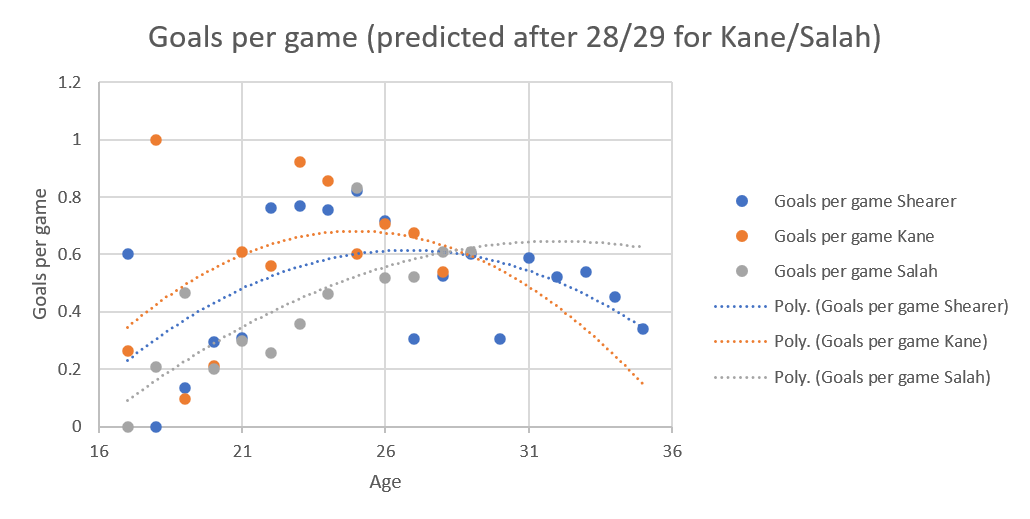 The shape of the three curves is quite different, Salah's constantly increasing, Shearer's a parabola, but a fairly shallow one, while Kane's is a much sharper parabola. I'm not sure if that's because of low goals per game last season skewing the whole curve, that frankly ridiculous season he had at 18 or a side effect of Spurs playing him slightly deeper now.
The shape of the three curves is quite different, Salah's constantly increasing, Shearer's a parabola, but a fairly shallow one, while Kane's is a much sharper parabola. I'm not sure if that's because of low goals per game last season skewing the whole curve, that frankly ridiculous season he had at 18 or a side effect of Spurs playing him slightly deeper now. 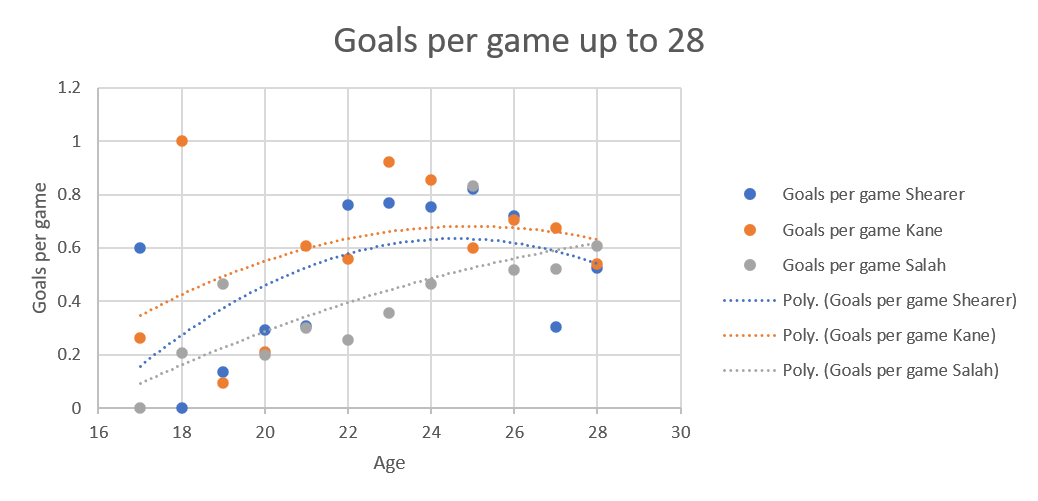
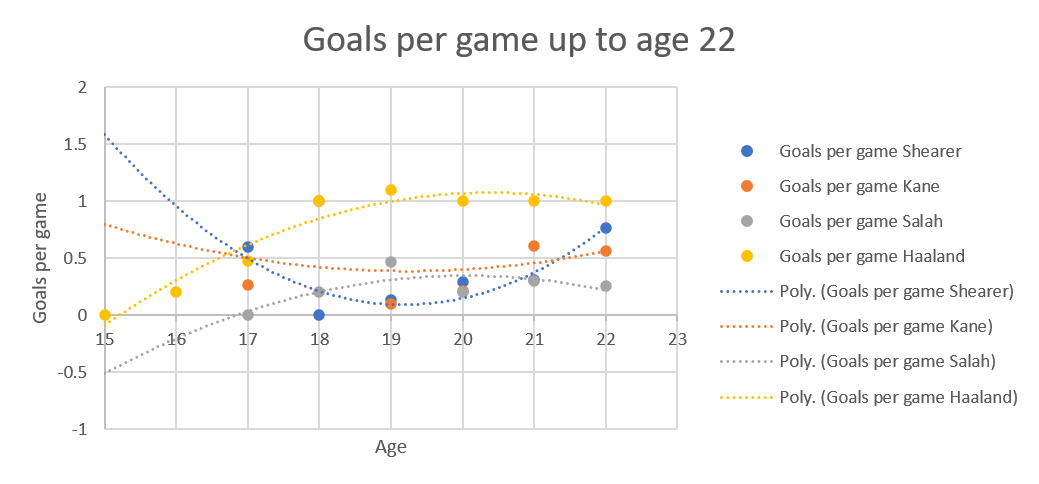
 which is unexpected. I would have expected deleterious effects to hit Kane and Salah equally but Kane's curve really is warped by the poor year at 27.
which is unexpected. I would have expected deleterious effects to hit Kane and Salah equally but Kane's curve really is warped by the poor year at 27. 
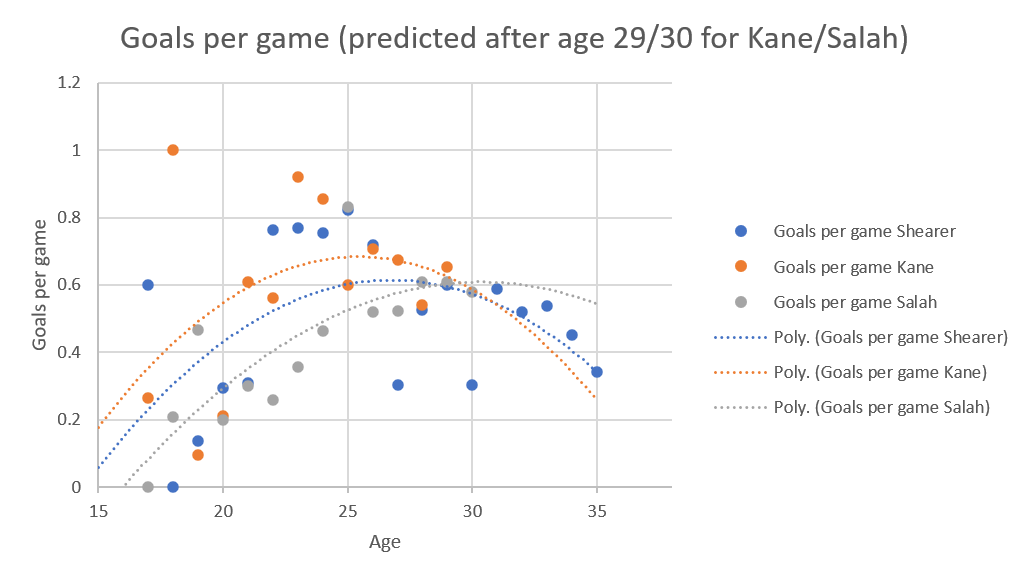
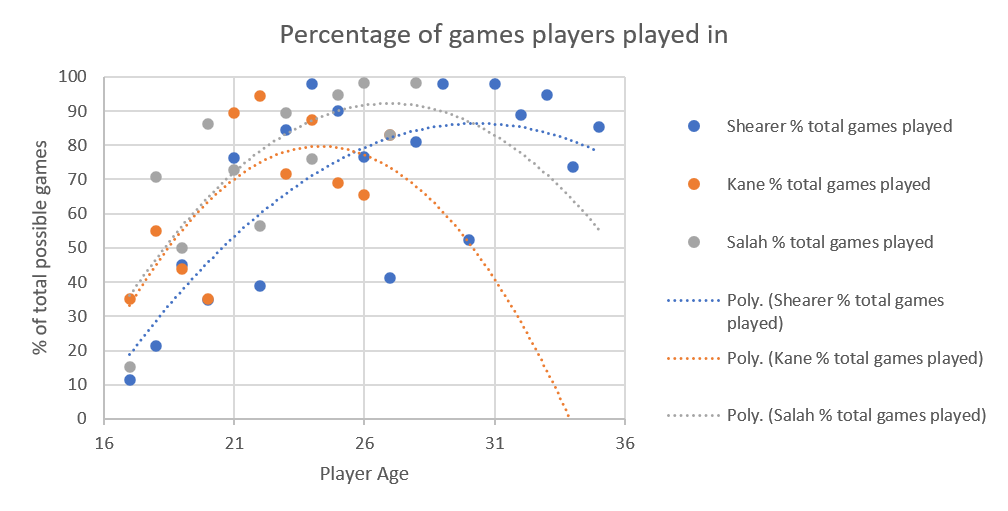
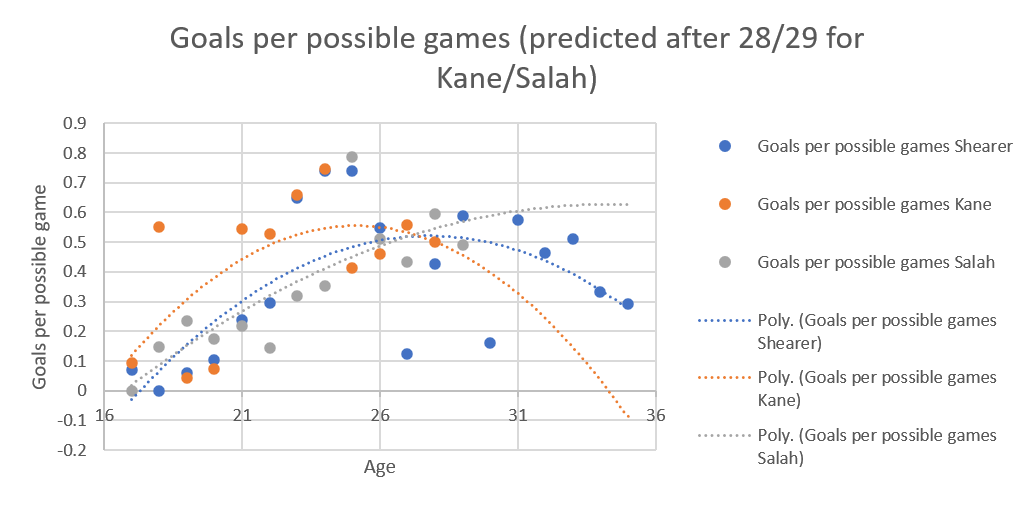 While it could be Kane's production dropping precipitously, I think it's the extrapolation because the curves without extrapolation look like this:
While it could be Kane's production dropping precipitously, I think it's the extrapolation because the curves without extrapolation look like this:
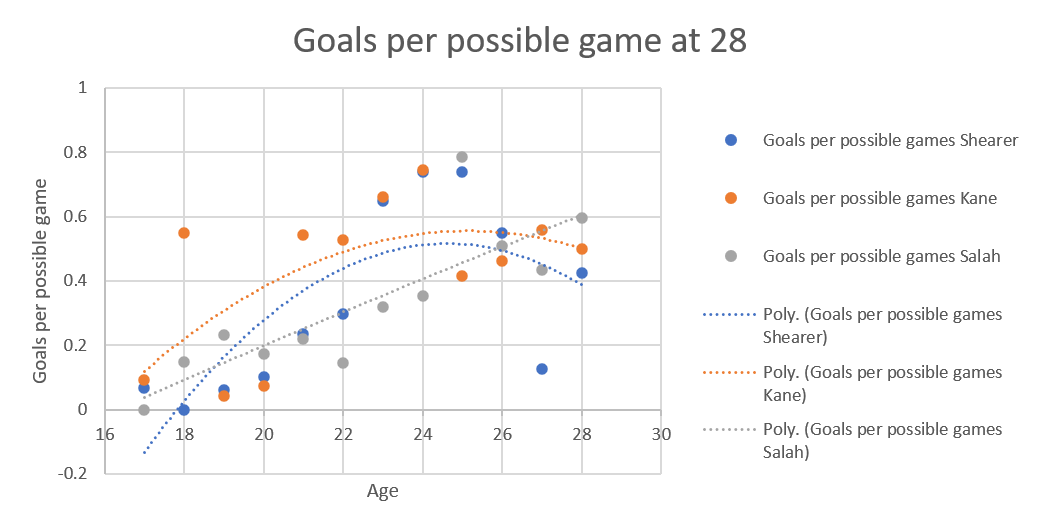 Where can this go? Well, there are 3 possible future things I'm thinking of looking at.
Where can this go? Well, there are 3 possible future things I'm thinking of looking at. 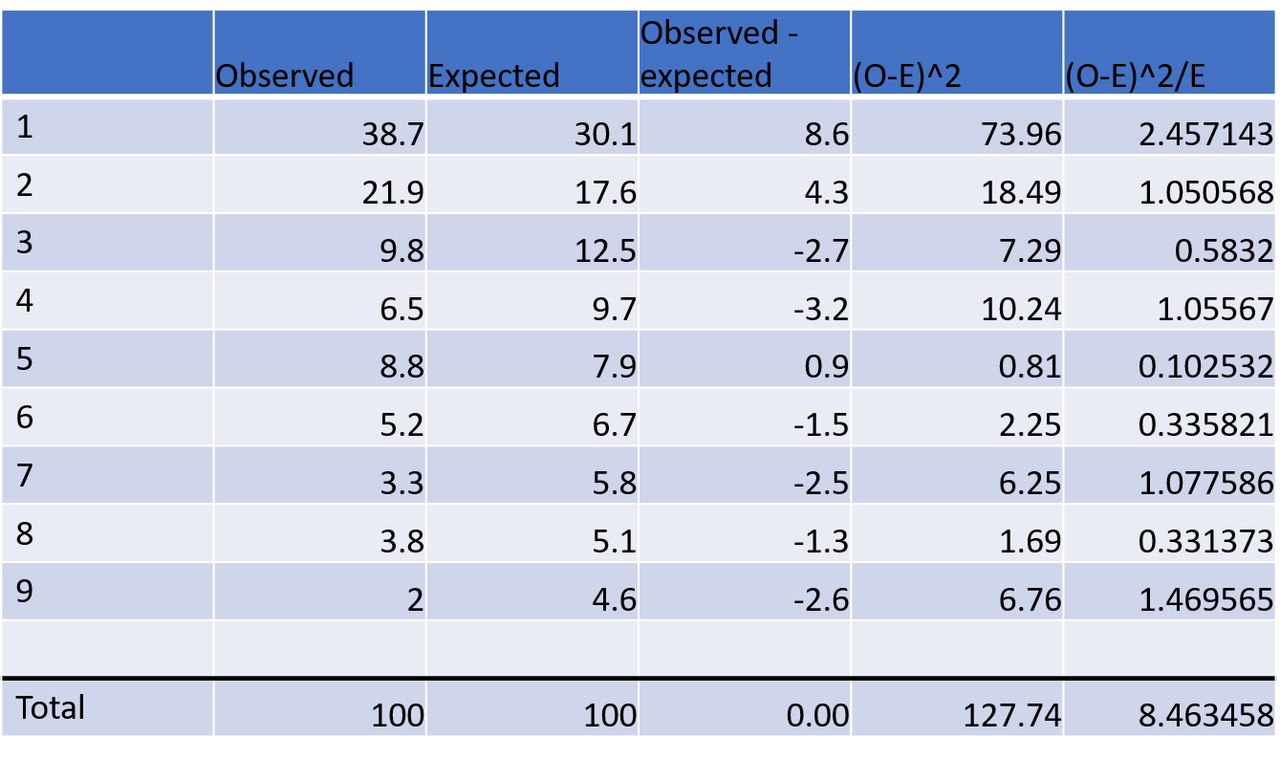
In June, I recorded the first digits in the top news article on the BBC website on 24/30 days. In those 24 articles, there were 353 numbers with leading digits. That's 14-15 per day, which is a lot more than in March, April and May, but about the same as in February.
2 is appearing the expected percentage of times. 1 and 8 are the most different to their expected values with 1 being over-represented and 8 under-represented. If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 4.9, the same as May.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.
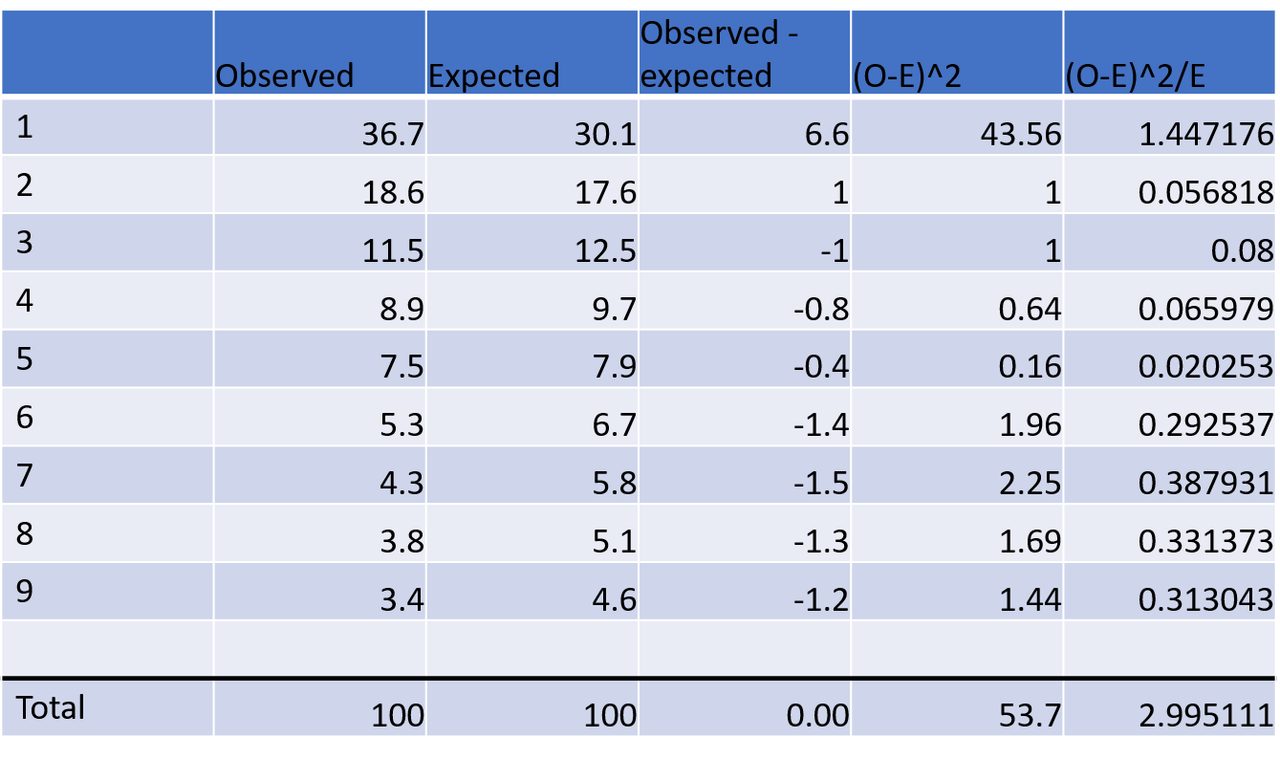
If we look at the rolling total from February to the end of June, there have been 1599 numbers with leading digits.
2 is exactly its expected value. 1 is the number furthest away from its expected value and remains over-represented, the next furthest away is 6 which is under-represented. If you add together the sum of all the values of (observed-expected) squared, all divided by the expected, the calculated test statistic is 2.71.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford’s Law.
This is a reduction from the test statistic of the total to May, but it's not as low as it was before May.
This follows the three previous posts.
I was better at remembering to add the daily article in May, adding articles on 29 of 31 days.
Looking at May's articles only, 313 leading digit numbers were used (10-11 per day, slightly more than April, about the same as March and less than February).
3 is appearing the expected percentage of times. 1 and 7 are the most different to their expected values wth 1 being over-represented and 7 under-represented. If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 6.67, slightly higher than April.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.
If we look at the rolling total from February to the end of May, there have been 1254 numbers with leading digits.
2 and 3 are the numbers closest to their expected values. 1 is the number furthest away from its expected value and remains over-represented, the next furthest away is 6 which is under-represented. If you add together the sum of all the values of (observed-expected) squared, all divided by the expected, the calculated test statistic is 2.84.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford’s Law.
Interestingly, as more numbers from articles added you would expect the calculated test statistic to reduce. Previously, it has (February = 8.6, February + March = 3.49, February + March + April = 2.29), but the test statistic has increased this time to 2.84, possibly explained by the articles from the 1st, 7th and 8th of May being very skewed towards the number 1 and having a lot of numbers in them.
This is the results of the third month of monitoring news articles for which numbers they contain.
I missed a couple more days in April, I blame Easter, and I will catch these up at the end of the year.
In the 27 days I did manage to capture, 232 numbers were used in the leading news articles on bbc.co.uk (~ 8 to 9 per day). This is slightly less than the 9-10 in March and a lot less than the 15 per day from February.
9 is the number closest to its expected value. 2 is over-represented, 8 is under-represented. If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 5.7.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.
If you look at the rolling total of February to the end of April, the numbers are starting to add up. Since the start of February, there have been 941 digits in headline news articles.
5 is the number closest to its expected value. 1 remains over-represented, while 6 is under-represented. If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 2.29.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.
Interestingly, as more numbers from articles have been added the calculated test statistic has reduced (February = 8.6, February + March = 3.49, February + March + April = 2.29). This is what you would expect to see if the numbers in the articles fulfill Benford's law.
This is the results of the second month of monitoring news articles for which numbers they contain.
March featured the first days I missed (I blame Easter), so I will have to add two days on at the end of the year.
In the 29 days I did manage to capture, 273 numbers were used (~ 9 to 10 per day). This is less than the ~15 per day from February.
1 and 8 are the closest to expected. 5 is over-represented. If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 5.6.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.
If you look at the rolling total of February and March, the numbers are starting to add up. There were 709 digits in headline news articles.
7 and 8 are the closest to expected. 1 remains over-represented, as it was in February. If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 3.49.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.
Interestingly, as more numbers from articles have been added the calculated test statistic has reduced (February = 8.6, February + March = 3.49). This is what you would expect to see if the numbers in the articles fulfill Benford's law.
Benford's Law gains its power with larger numbers, and I started my Benford's law project in the shortest month. I don't think these things through, do I? But you have to start somewhere.
The 28 daily news articles contained 436 numbers written as digits (~15 per day).
3 and 7 are found pretty much exactly as often as expected. 1 is over represented.
If you add together the sum of all the values of (observed-expected)squared, all divided by the expected, the calculated test statistic is 8.6.
The critical chi squared value for 9 items with only one line is ~ 15.507
The test statistic smaller than the critical value therefore the difference is not significant. This data does not disobey Benford's Law.*
*That noise is L shouting "obey is the word you want" but to me there's a difference between 'stats show x' and 'stats show not x' and to me, these show 'do not disobey'.
Introduction:
Some years ago, I read the book, “How Long Is a Piece of String?: More Hidden Mathematics of Everyday Life by Rob Eastaway” (as reviewed here), and one chapter fascinated me. The chapter was chapter 12 - “Is it a fake?”, and the section that particularly caught my interest was about Benford’s Law. Excessively simplifying, in naturally occurring numbers, the leading digits will follow a distinct pattern, and will not be randomly distributed.
The expected % of leading numbers for each digit can be seen in the table below:
If you have a large naturally occurring data set that doesn’t conform to this, it tells you there are either constraints on it so that the data doesn’t cover all of the possibilities (e.g. human heights in m are will start with a 1 or a 2, no one has ever been 4 m tall) or something else is going on.
Testing this theory:
I wanted to test this out on *something*. Problem was, what? Most sports data is possibility-limited e.g. fewer goals will be scored in football the 9th or 9xths minute than would be scored in the 8th and 8xths minute, not because of the minute, but because the game stops at the 90th minute. Other data isn’t big enough. I needed a source of numbers that was large and unlimited.
Eventually, possibly in a fit of cynicism, I decided to try the leading digits of numbers reported in the news. Advantages to this plan - I can use a single, traceable data source - one article a day from the BBC news website. The BBC doesn’t tend to delete pages so if someone wanted to double check my numbers, I could give them the links.
Disadvantages to this plan - when I first attempted it, Article 50 was in the news, and skewing my results.
Having looked at the results, and realised this and a few methodological errors, and going a bit stir-crazy because of lockdown 3, I decided to try it again.
Attempt Number 2:
These were the rules I developed to try to avoid that and similar pitfalls:
1 - no numbers in names e.g. 19 in COVID-19 does not count as a leading digit
2 - no numbers from dates (I had done this originally, but worth restating)
3 - only digits written as digits. This threw up an unexpected problem - the BBC has somewhat intermittent editorial control on whether digits under 10 are written as words or numbers, and this may skew results. I’ve saved the links to the articles I’ve used to put the project together so I can go through them again if I want to (or if someone else wants to look at them).
I started on the 1st of February 2021, and will carry on till 1st of February 2022 (barring disaster). The other advantage of this system is that if I miss a day, I can fill them in with more days at the end. I will give monthly updates and running totals, plus some commentary if I have any.
In 2019, Formula 1 introduced a bonus point for the driver who sets the fastest lap at each race (1 point for the driver, 1 point for the constructor). They added some conditions, the point would only be given to a driver in the top 10 - if someone outside the top 10 sets the fastest lap, no point is awarded. That struck me as unfair because it's down amongst the bottom half of the constructors’ championship where that extra point will count at the end of the season, especially when it comes to the money given to the teams.
That's part of the problem, the idea seemed to have been to encourage the teams to do something in the often dead last quarter of the race, when the interesting part of the race is over because the cars are too wide to allow overtaking at most tracks and there's no more pitstops to permit over/under cuts. Having cars come in for fresh tyres towards the end of the race to aim for the fastest lap point is supposed to increase interest, rather than being a bad sign that there's enough distance between cars to allow for a pitstop without a loss of place. But at the same time, they didn't want it to have too big an effect, because we'd never hear the end of it if someone won the World title purely because of fastest lap points.
Overall, I doubt adding fastest lap changes that much (and everyone knows how I feel about pointless changes) so I decided to go through the last 10 years’ worth of results (okay 11, because this happened in 2019, and I'm only writing this in 2020) and see if it does change anything. For 2009-2018, would adding fastest lap points change either the drivers’ or constructors’ standings at the end of the season, for 2019 and 2020, would removing them change anything. Because there'll be a lot of numbers, I'm putting them in separate posts and linking to them at various points.
Before anyone else says anything about them, yes there are caveats. Before fastest lap points became a thing, drivers may not have bothered to go for fastest laps because they were worth nothing (except bragging rights, and bragging rights should never be underestimated), therefore it is a slightly artificial experiment.
The results
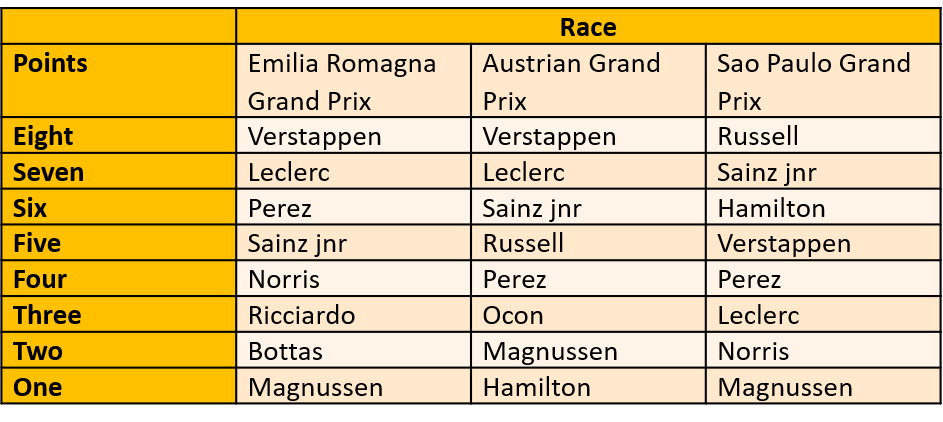
2009 (link to results here). To no-one’s surprise, Mark Webber was one of the first drivers who wouldn’t have got a fastest lap because of finishing outside the top 10. He finished outside the top 10 when he was fastest at the Japanese Grand Prix. The shock is that the perpetually cursed-with-bad-luck Webber was not the first person this happened to, no, that would have been Timo Glock at the European Grand Prix. Nine different drivers (ten if you want to count Glock) different drivers, driving for seven different constructors, would have gained points.
There would be no changes to the standings in the constructors’ title, and only 16th and 17th place would swap in the drivers’ standings.
For 2010 (link here), three races would have had no fastest lap point awarded. Six different drivers (or seven counting Petrov who didn’t finish in the top 10 when he set the fastest lap at the Turkish Grand Prix) for four manufacturers would have received fastest lap points. There would have been no changes to either the Drivers’ or Constructors’ Championship standings.
2011 (link here) would have been the first season that a fastest lap point would have been awarded at each grand prix, because all the people who set fastest laps finished in the top 10 of each particular race. Six drivers for three teams would have won fastest lap points. However, it would have had no effect on final standings.
2012 (link here) was much more of a mixed bag. Four races would not have seen fastest lap points awarded because the person who set the fastest lap either didn’t finish in the top ten or didn’t finish at all. Even with that, 8 drivers from 5 teams would have won fastest lap points (the unawarded ones raises that to 12 drivers and 7 teams). This makes no difference to the Constructors’ Championship, but does cause a small movement in the Drivers’ Championship. In the real world, Lewis Hamilton finished in 4th on 190 points, with Jenson Button finishing in 5th on 188 points. In our counter-factual universe, where fastest lap points are awarded, Hamilton won none of these (the one race where he set a fastest lap, he did not finish), Button won two, and therefore, they are tied on 190 points. It then goes to count back. Both drivers won three races, but Button’s next best finish, 2nd, is better than Hamilton’s next best, 3rd. Therefore, Button move into 4th and Hamilton is knocked down to 5th.
There are no changes due to the award of fastest lap point in 2013 (link here). All but one race would have seen a point awarded (Esteban Gutierrez unluckily finishing in 11th at the Spanish Grand Prix). Six drivers from five teams would have won fastest lap point (seven from six teams if Gutierrez had been luckier). However, nothing would have changed in the Constructors’ or Drivers’ Championships.
2014, or the year of the silly attempt to add excitement by awarding double points. (Is it really 6 years since I wrote about that nonsense? I didn’t like it then, and I am glad they got rid of it.) If fastest lap points had been awarded in 2014 according to the rules now in use, nothing would have changed with the final positions, 17 out of the 19 races would have seen points awarded, for 6 drivers from 4 teams.
If points had been awarded to all drivers who set a fastest lap, regardless of final position, something would have changed. Kimi Räikkönen was one of the two drivers who set fastest laps, but would not have been awarded a point because he finished outside the top 10 (at the Monaco Grand Prix in his case). If he had been awarded a point, he would have leapt into 11th place in the drivers’ championship, ahead of Kevin Magnussen, but since the point wouldn’t have been awarded, this is another season where the fastest lap points would have changed nothing. Full details here.
Fewer drivers would have won fastest lap points in 2015 (link here), with only 5 drivers for 3 different teams setting fastest laps. While this doesn’t change anything in the constructors’ championship, fastest lap points would have moved Daniel Ricciardo up to 7th place in the drivers’ championship, ahead of Daniil Kvyat. With the addition of fastest lap points, Ricciardo and Kvyat would have the same number of points, and, although their best result is the same (one second place each), Ricciardo’s next best result is better than Kvyat’s next best result (a third place vs a fourth).
Two races in 2016 would not have seen points awarded, with Nico Hülkenberg missing out due to finishing 15th at the Chinese Grand Prix, and Fernando Alonso missing out due to finishing 14th at the Italian Grand Prix. Fastest lap points would have been awarded to seven drivers from four teams (it would have been nine drivers from six teams if points were awarded no matter the finishing position). There are no changes in the drivers’ or constructors’ championships, and the only thing the fastest lap point would have done would be to increase the gap between Rosberg and Hamilton at the end of the season. Full details here.
Seven drivers would have received fastest lap points (it would have been eight but Sergio Perez finished in 13th at the Monaco Grand Prix), for four different constructors (would have been five if Perez had been given the point) in 2017. There would have been no changes to the constructors’ or drivers’ championships (details here).
In the 2018 season, two races would not have seen points awarded, Valtteri Bottas finished in 14th at the Azerbaijan Grand Prix, while Kevin Magnussen finished in 18th at the Singapore Grand Prix. Personally, I say if somehow, anyone manages to get a Haas to be the fastest car of a race, they ought to receive a point, but that’s not what the rules state. Adding fastest laps does not change anything in the constructors’ Championship. In the drivers’s championship, Bottas would have moved into 3rd from 5th, with Verstappen narrowly missing out on passing Räikkönen for what would now be 4th. (Full details here)
This was the year where Force India had to reconstitute themselves mid-season. Fastest lap points do not change either of their positions. Obviously, if both “Force India”s points were added together, they race up the constructors’ championship but adding fastest lap points wouldn’t change that amalgamated table either.
Now we come to the second half of this accidental natural experiment, 2019 and 2020, years in which fastest lap points were awarded. For these two seasons the question is, will positions change with fastest lap points removed.
2019 – Six drivers from three teams won fastest lap points, both members of the three big teams. Two races didn’t see fastest lap points, because Kevin Magnussen finished in 17th at the Singapore Grand Prix and Bottas DNF at the Brazilian Grand Prix. Again, I would like to state my policy that if anyone manages to get a Haas to be the fastest car of a race, they ought to receive a point (although giving Magnussen that point wouldn’t have changed anything in the drivers’ championship). (Details here)
2020 was a weird season in a weird year. Fastest driver points were awarded in all 17 Grand Prix. They were awarded to 7 drivers across 4 teams (details here). Removing fastest lap points makes no difference to the Constructor’s title (don’t look at the constructors table, it is a thing of horror for all Ferrari fans). In the Drivers’s championship, removal of the fastest lap points would move Albon ahead of Carlos Sainz jnr, but I am not sure that would have saved his seat, Red Bull being what they are.
Conclusion:
So, what have we established? At no point did adding or removing fastest lap points change the standings in the Constructors’ Championship.
0/129 placings.
0%.
Zero.
Zulu. Echo. Romeo. Oscar.
[add in other languages, as applicable]
This established, let's look at the Drivers’ Championship: 11 drivers would have changed the finishing position with the addition or removal of fastest lap points (11/284 = 3.9%).
However, none of these changes would affect who won the title, and since I’m not party to individual contracts; I don’t know if anyone would have made some extra money or if anyone missed out on some cash.
Mostly, this has been a change that affected nothing, but why is this? Partly it’s the small size of the “fastest lap bonus”: a single point compared to the 25 points for a win.
I think they made it deliberately small so it wouldn’t affect the big things like the Drivers’ championship, but it’s so small that it doesn’t affect anything in the Constructors Standings (where money is more obviously at stake).
While I disapprove of change for change's sake; I don’t think those in charge will get rid of the fastest lap point in the short term because it gives the appearance of excitement, gives the commentators something to talk about in the dead space after the pitstops.
I’d rather they tweak the rules to give spectators more exciting racing; but I don’t think I’m getting that any time soon either.